From the September 3, 2025 issue of the Raven
A Chance Encounter
Over the last ten years of intensive focus on Franconia Ridge I have come to refer to the surge of hikers and runners that stewards see on popular weekend days as “the wave.” During seminars and while doing field work this year, students and trails fellows began to expand this analogy, seeing hikers “flow” across the Ridge and summits and pullouts as “eddies.”
A chance encounter on Franconia Ridge almost two weeks ago sparked me to take this analogy to a new level. I met a hiker whose field of expertise is in biosignal processing and nonlinear systems analysis, who studies physiological flows like heart rhythms and arterial turbulence. We corresponded after, and he asked if I thought the Navier–Stokes equations might apply to trails.

The Navier–Stokes equations are the fundamental mathematical description of how fluids (like air or water) move, capturing the balance between inertia, pressure, viscosity, and external forces. That question encouraged me to pull together a few ideas I’ve been developing over the decade and consider how this analogy might help us build a model for off-trail surges on Franconia Ridge.
Fluid Dynamics as Analogy
The Navier–Stokes equation can be a surprisingly useful analogy for hiker flow. At its core, fluid dynamics helps us think about how many individual “particles” moving together generate collective patterns like laminar flow, turbulence, eddies, and surges. Those patterns map well onto what we see on high-use trails: smooth movement when hikers are well spaced, congestion when they bunch up, and sudden bursts of off-trail departures when local density rises too high.
From Pipes, to Arteries, to Rivers
Pipes are rigid: too much pressure and they burst, too little and they collapse (Venturi effect). This is a binary, mechanical mode of failure — the pipe is intact, or it has catastrophically failed.
Arteries are elastic: adaptive, but also prone to nonlinear thresholds. Turbulence interacts with narrowing walls, so small changes in flow can lead to sudden constriction or occlusion. This resembles the way off-trail departures spike once density passes a tipping point (Lee et al., 2012).
Rivers are adaptive: porous banks allow flow to respond to terrain, and excess volume produces meanders and braids. Trails behave the same way: instead of bursting, they widen and braid under pressure (Wimpey & Marion, 2010).
This progression — pipe, artery, river — shows why rivers may be our best analogy, while physiology reinforces why nonlinear thresholds must be central to our models.
Thresholds and Nonlinear Dynamics on Franconia Ridge
Field observations align with this systems view. On busy weekends, the sequence:
→ A morning wave of hikers enters the loop, creating a density surge that moves across the Ridge like a flood pulse → At first, flow remains laminar: hikers stay mostly on-trail → Once a density threshold is exceeded, behavior changes suddenly: hikers step off to pass, to rest, or to avoid crowds → Off-trail departures spike nonlinearly, resembling a bifurcation event (Helbing et al., 2000) → Impacts grow disproportionately: a modest increase in hikers per hour results in a dramatic rise in trampling and braiding.
This is the hallmark of a complex adaptive system. Like turbulence in arteries or overbank flooding in rivers, trail impacts emerge abruptly once thresholds are crossed.
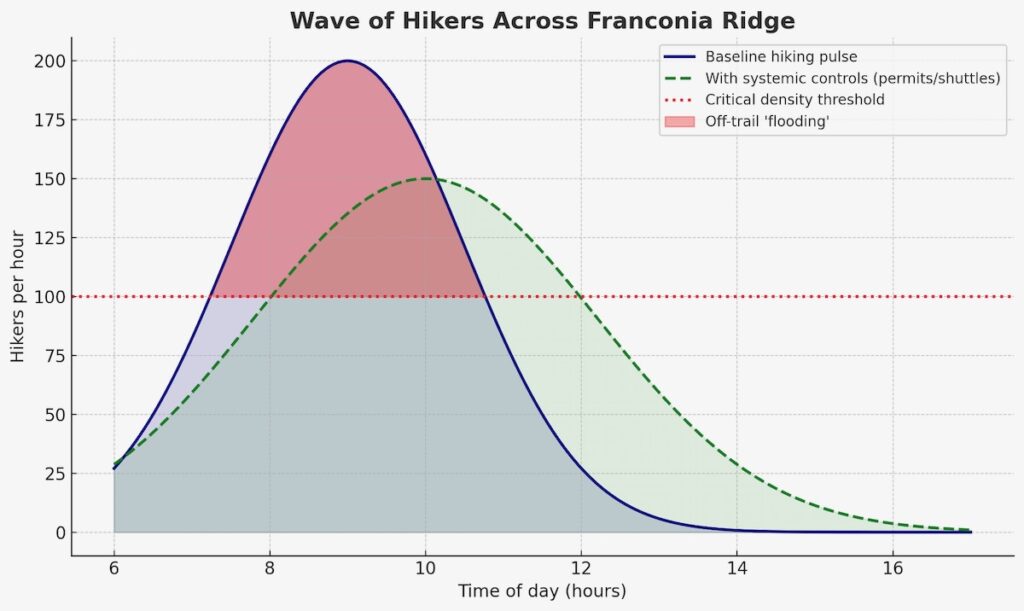
Using Agent-Based Modeling to Anticipate Outcomes
Because averages obscure these nonlinear spikes, managers need modeling approaches that capture thresholds and feedback. Agent-based modeling (ABM) offers a promising tool.
How it works: each hiker is modeled as an “agent” with simple rules — walking speed, group size, comfort with crowding, probability of stepping off-trail under certain densities or slopes.
Wave dynamics: by varying start times at trailheads, the model can simulate the morning “pulse” of hikers moving across the Ridge, showing when and where local densities approach critical thresholds.
Threshold behaviors: ABM has already been used in visitor management for protected areas (Štekerová et al., 2022) and in crowd science to capture nonlinear “panic” or “jam” effects (Helbing et al., 2000). Similar approaches have shown how social groupings change crowd flow (Moussaïd et al., 2010) and how physiological factors shape pedestrian trajectories (Narang et al., 2015).
Testing interventions: scenarios can be run for permit or timed-entry systems, steward placement at key “eddies,” trail design changes, or communication tools like signage and steward contact.
This mirrors river management, where levees, diversions, and floodplains work together. It also reflects physiology, where resilience depends on both vessel walls and regulatory signals.

A Systemic View of the Loop
The river analogy encourages managers to take a whole-system view of the Franconia Ridge loop:
Inputs: parking, shuttles, and trailhead access determine the size and timing of the hiker “wave.”
Regulation: permits, timed-entry systems, shuttle timing can flatten the morning surge, lowering the chance of threshold crossing.
Trail design: side-hill alignment, wider trails, scree walls, string fencing.
Local controls: stewards act as “regulators,” dampening turbulence at critical points and educating visitors.
Above treeline, where realignment away from fall-line routes may not be feasible, these systemic and social interventions are crucial to protecting the three miles of alpine zone on the Franconia Ridge Loop that are most at risk.
Conclusion
Trails behave less like pipes waiting to burst and more like rivers whose channels expand and braid under pressure. The artery analogy reminds us why thresholds matter: small changes can trigger nonlinear shifts with outsized impacts.
By adopting this systemic, nonlinear perspective, managers can better anticipate surges, identify bifurcation points, and deploy layered interventions. This is the essence of Integrated Trail Management (ITM): combining design, education, regulation, and stewardship to create resilience in the face of growing use.
Just as rivers are managed through levees, diversions, and floodplains, and arteries rely on both vessel strength and systemic regulation, Franconia Ridge can be managed through a mix of direct and indirect tools. The goal is not to eliminate flow, but to channel it wisely, preserving fragile alpine ecosystems.
Looking ahead, agent-based modeling (ABM) can help managers simulate how hikers move across the Ridge, anticipate where thresholds are crossed, and test interventions virtually before applying them on the ground. By linking trail design, administrative tools (permits, timed entry, shuttle schedules), and policy measures (group size limits, steward placement) into a single systemic framework, ABM provides a way to identify the most effective combinations. In this way, science, design, and governance reinforce one another — giving us a path toward both protecting the alpine zone and sustaining the experience of those who visit it.
References
Cole, D.N. (1995). Experimental trampling of vegetation: Predictors of resistance and resilience. Journal of Applied Ecology, 32, 215–224.
Helbing, D., Farkas, I., & Vicsek, T. (2000). Simulating dynamical features of escape panic. Nature, 407, 487–490. https://doi.org/10.1038/35035023
Marion, J.L. (2016). A review and synthesis of recreation ecology research supporting carrying capacity and visitor use management decisionmaking. Journal of Forestry, 114(3), 339–351.
Marion, J.L., Park, L.O., & Wimpey, J. (2022). Efficacy of Combining Education and Site Management in Reducing Off-Trail Travel in a Fragile Biotic Community, Acadia National Park. Journal of Interpretation Research, 28(1), 26–45.
Moussaïd, M., Perozo, N., Garnier, S., Helbing, D., & Theraulaz, G. (2010). The walking behaviour of pedestrian social groups and its impact on crowd dynamics. PLoS One, 5(4), e10047. https://doi.org/10.1371/journal.pone.0010047
Narang, S., Best, A., Curtis, S., & Manocha, D. (2015). Generating pedestrian trajectories consistent with the fundamental diagram based on physiological and psychological factors. PLoS One, 10(4), e0117856. https://doi.org/10.1371/journal.pone.0117856
Park, L.O., Manning, R.E., Marion, J.L., Lawson, S.R., & Jacobi, C. (2008). Managing visitor impacts in parks: A multi-method study of the effectiveness of alternative management practices. Journal of Park and Recreation Administration, 26(1), 97–121.
Rupf, R., Haegeli, P., Karlen, B., & Wyttenbach, M. (2019). Does Perceived Crowding Cause Winter Backcountry Recreationists to Displace? Mountain Research and Development, 39(1), R60.
Štekerová, K., Zelenka, J., & Kořínek, M. (2022). Agent-Based Modelling in Visitor Management of Protected Areas. Sustainability, 14(19), 11853. https://doi.org/10.3390/su141911853
Lee, J., Nemati, S., Silva, I., Edwards, B.A., Butler, J.P., & Malhotra, A. (2012). Transfer entropy estimation and directional coupling change detection in biomedical time series. Biomedical Engineering Online, 11(1), 19. https://doi.org/10.1186/1475-925X-11-19
Wimpey, J., & Marion, J.L. (2010). The influence of use, environmental and managerial factors on the width of recreational trails. Journal of Environmental Management, 91(9), 2028–2037. https://doi.org/10.1016/j.jenvman.2010.05.017
